2.2.5.3.- DATA MINING O MINERÍA DE DATOS
2.2.5.3.2.- Técnicas de Data Mining
2.2.5.3.3.- Metodología de aplicación
2.2.5.3.1.-Introducción
El Data Mining es un proceso que, a través del descubrimiento y cuantificación de relaciones predictivas en los datos, permite transformar la información disponible en conocimiento útil de negocio. Esto es debido a que no es suficiente "navegar" por los datos para resolver los problemas de negocio, sino que se hace necesario seguir una metodología ordenada que permita obtener rendimientos tangibles de este conjunto de herramientas y técnicas de las que dispone el usuario.
Constituye por tanto una de las vías clave de explotación del Data Warehouse, dado que es este su entorno natural de trabajo.
Se trata de un concepto de explotación de naturaleza radicalmente distinta a la de los sistemas de información de gestión, dado que no se basa en coeficientes de gestión o en información altamente agregada, sino en la información de detalle contenida en el almacén. Adicionalmente, el usuario no se conforma con la mera visualización de datos, sino que trata de obtener una relación entre los mismos que tenga repercusiones en su negocio.
2.2.5.3.2.Técnicas de Data Mining
Para soportar el proceso de Data Mining, el usuario dispone de una extensa gama de técnicas que le pueden ayudar en cada una de las fases de dicho proceso, las cuales pasamos a describir:
Análisis estadístico:
Utilizando las siguientes herramientas:
- ANOVA: o Análisis de la Varianza, contrasta si existen diferencias significativas entre las medidas de una o más variables continuas en grupo de población distintos.
- Regresión: define la relación entre una o más variables y un conjunto de variables predictoras de las primeras.
- Ji cuadrado: contrasta la hipótesis de independencia entre variables.
- Componentes principales: permite reducir el número de variables observadas a un menor número de variables artificiales, conservando la mayor parte de la información sobre la varianza de las variables.
- Análisis cluster: permite clasificar una población en un número determinado de grupos, en base a semejanzas y desemejanzas de perfiles existentes entre los diferentes componentes de dicha población.
- Análisis discriminante: método de clasificación de individuos en grupos que previamente se han establecido, y que permite encontrar la regla de clasificación de los elementos de estos grupos, y por tanto identificar cuáles son las variables que mejor definan la pertenencia al grupo.
Métodos basados en árboles de decisión:
El método Chaid (Chi Squared Automatic Interaction Detector) es un análisis que genera un árbol de decisión para predecir el comportamiento de una variable, a partir de una o más variables predictoras, de forma que los conjuntos de una misma rama y un mismo nivel son disjuntos. Es útil en aquellas situaciones en las que el objetivo es dividir una población en distintos segmentos basándose en algún criterio de decisión.
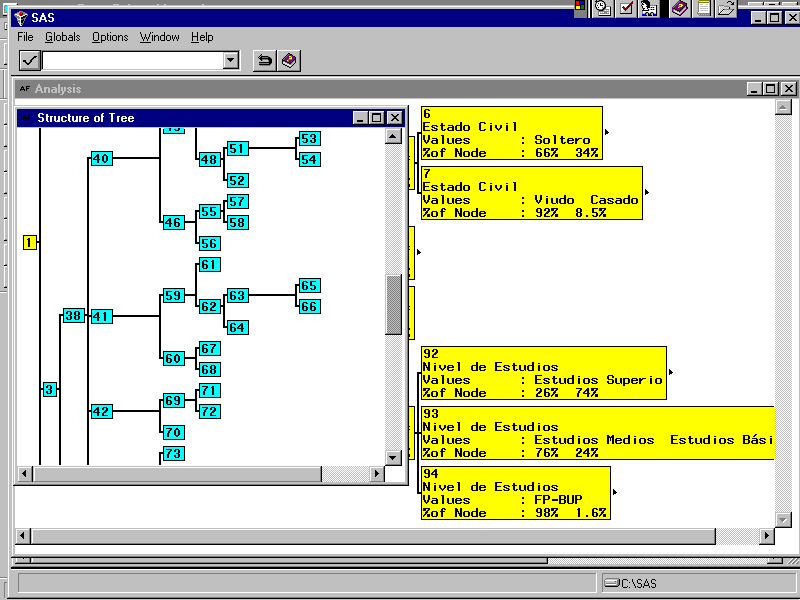
El árbol de decisión se construye partiendo el conjunto de datos en dos o más subconjuntos de observaciones a partir de los valores que toman las variables predictoras. Cada uno de estos subconjuntos vuelve después a ser particionado utilizando el mismo algoritmo. Este proceso continúa hasta que no se encuentran diferencias significativas en la influencia de las variables de predicción de uno de estos grupos hacia el valor de la variable de respuesta.
La raíz del árbol es el conjunto de datos íntegro, los subconjuntos y los subsubconjuntos conforman las ramas del árbol. Un conjunto en el que se hace una partición se llama nodo.
El número de subconjuntos en una partición puede ir de dos hasta el número de valores distintos que puede tomar la variable usada para hacer la separación. La variable de predicción usada para crear una partición es aquella más significativamente relacionada con la variable de respuesta de acuerdo con test de independencia de la Chi cuadrado sobre una tabla de contingencia.
Algoritmos genéticos:
Son métodos numéricos de optimización, en los que aquella variable o variables que se pretenden optimizar junto con las variables de estudio constituyen un segmento de información. Aquellas configuraciones de las variables de análisis que obtengan mejores valores para la variable de respuesta, corresponderán a segmentos con mayor capacidad reproductiva. A través de la reproducción, los mejores segmentos perduran y su proporción crece de generación en generación. Se puede además introducir elementos aleatorios para la modificación de las variables (mutaciones). Al cabo de cierto número de iteraciones, la población estará constituida por buenas soluciones al problema de optimización.
Redes neuronales:
Genéricamente son métodos de proceso numérico en paralelo, en el que las variables interactúan mediante transformaciones lineales o no lineales, hasta obtener unas salidas. Estas salidas se contrastan con los que tenían que haber salido, basándose en unos datos de prueba, dando lugar a un proceso de retroalimentación mediante el cual la red se reconfigura, hasta obtener un modelo adecuado.
Lógica difusa:
Es una generalización del concepto de estadística. La estadística clásica se basa en la teoría de probabilidades, a su vez ésta en la técnica conjuntista, en la que la relación de pertenencia a un conjunto es dicotómica (el 2 es par o no lo es). Si establecemos la noción de conjunto borroso como aquel en el que la pertenencia tiene una cierta graduación (¿un día a 20ºC es caluroso?), dispondremos de una estadística más amplia y con resultados más cercanos al modo de razonamiento humano.
Series temporales:
Es el conocimiento de una variable a través del tiempo para, a partir de ese conocimiento, y bajo el supuesto de que no van a producirse cambios estructurales, poder realizar predicciones. Suelen basarse en un estudio de la serie en ciclos, tendencias y estacionalidades, que se diferencian por el ámbito de tiempo abarcado, para por composición obtener la serie original. Se pueden aplicar enfoques híbridos con los métodos anteriores, en los que la serie se puede explicar no sólo en función del tiempo sino como combinación de otras variables de entorno más estables y, por lo tanto, más fácilmente predecibles.
2.2.5.3.3. Metodología de aplicación:
Para utilizar estas técnicas de forma eficiente y ordenada es preciso aplicar una metodología estructurada, al proceso de Data Mining. A este respecto proponemos la siguiente metodología, siempre adaptable a la situación de negocio particular a la que se aplique:
Muestreo
Extracción de la población muestral sobre la que se va a aplicar el análisis. En ocasiones se trata de una muestra aleatoria, pero puede ser también un subconjunto de datos del Data Warehouse que cumplan unas condiciones determinadas. El objeto de trabajar con una muestra de la población en lugar de toda ella, es la simplificación del estudio y la disminución de la carga de proceso. La muestra más óptima será aquella que teniendo un error asumible contenga el número mínimo de observaciones.
En el caso de que se recurra a un muestreo aleatorio, se debería tener la opción de elegir
- El nivel de confianza de la muestra (usualmente el 95% o el 99%).
- El tamaño máximo de la muestra (número máximo de registros), en cuyo caso el sistema deberá informar del el error cometido y la representatividad de la muestra sobre la población original.
- El error muestral que está dispuesto a cometer, en cuyo caso el sistema informará del número de observaciones que debe contener la muestra y su representatividad sobre la población original.
Para facilitar este paso s debe disponer de herramientas de extracción dinámica de información con o sin muestreo (simple o estratificado). En el caso del muestreo, dichas herramientas deben tener la opción de, dado un nivel de confianza, fijar el tamaño de la muestra y obtener el error o bien fijar el error y obtener el tamaño mínimo de la muestra que nos proporcione este grado de error.
Exploración
Una vez determinada la población que sirve para la obtención del modelo se deberá determinar cuales son las variables explicativas que van a servir como "inputs" al modelo. Para ello es importante hacer una exploración por la información disponible de la población que nos permita eliminar variables que no influyen y agrupar aquellas que repercuten en la misma dirección.
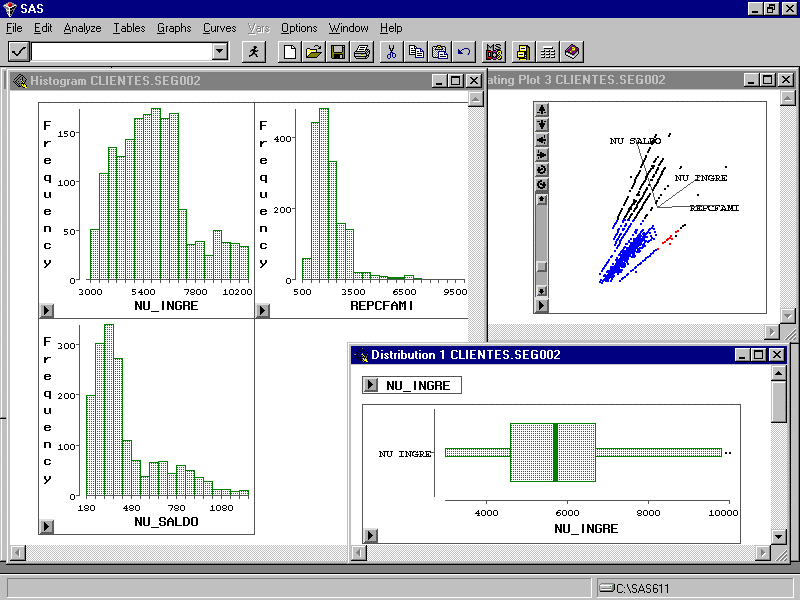
El objetivo es simplificar en lo posible el problema con el fin de optimizar la eficiencia del modelo. En este paso se pueden emplear herramientas que nos permitan visualizar de forma gráfica la información utilizando las variables explicativas como dimensiones.
También se pueden emplear técnicas estadísticas que nos ayuden a poner de manifiesto relaciones entre variables. A este respecto resultará ideal una herramienta que permita la visualización y el análisis estadístico integrados
Manipulación
Tratamiento realizado sobre los datos de forma previa a la modelización, en base a la exploración realizada, de forma que se definan claramente los inputs del modelo a realizar (selección de variables explicativas, agrupación de variables similares, etc.).
Modelización
Permite establecer una relación entre las variables explicativas y las variables objeto del estudio, que posibilitan inferir el valor de las mismas con un nivel de confianza determinado.
Valoración
Análisis de la bondad del modelo contrastando con otros métodos estadísticos o con nuevas poblaciones muestrales.


