2.1. Construcciones basicas
2.1. Construcciones basicas Dataprix 28 Septiembre, 2009 - 09:362.1.1. Entidades, atributos e interrelaciones
2.1.1. Entidades, atributos e interrelaciones Dataprix 28 Septiembre, 2009 - 10:24Por entidad entendemos un objeto del mundo real que podemos distinguir del resto de objetos y del que nos interesan algunas propiedades.Ejemplos de entidad
Algunos ejemplos de entidad son un empleado, un producto o un despacho. También son entidades otros elementos del mundo real de interés, menos tangibles pero igualmente diferenciables del resto de objetos; por ejemplo, una asignatura impartida en una universidad, un préstamo bancario, un pedido de un cliente, etc.
Las propiedades de los objetos que nos interesan se denominan atributos.Ejemplos de atributo
Sobre una entidad empleado nos puede interesar, por ejemplo, tener registrados su DNI, su NSS, su nombre, su apellido y su sueldo como atributos.
El término entidad se utiliza tanto para denominar objetos individuales como para hacer referencia a conjuntos de objetos similares de los que nos interesan los mismos atributos; es decir, que, por ejemplo, se utiliza para designar tanto a un empleado concreto de una empresa como al conjunto de todos los empleados de la empresa. Más concretamente, el término entidad se puede referira instancias u ocurrencias concretas (empleados concretos) o a tipos o clases de entidades (el conjunto de todos los empleados).
El modelo ER proporciona una notación diagramática para representar gráficamente las entidades y sus atributos:
• Las entidades se representan con un rectángulo. El nombre de la entidad se escribe en mayúsculas dentro del rectángulo.
• Los atributos se representan mediante su nombre en minúsculas unido con un guión al rectángulo de la entidad a la que pertenecen. Muchas veces, dado que hay muchos atributos para cada entidad, se listan todos aparte del diagrama para no complicarlo.
Cada uno de los atributos de una entidad toma valores de un cierto dominio o conjunto de valores. Los valores de los dominios deben ser atómicos; es decir,no deben poder
ser descompuestos. Además, todos los atributos tienen que ser univaluados. Un atributo es univaluado si tiene un único valor para cada ocurrencia de una entidad.
| Notación diagramática de entidades y atributos |
| La figura muestra la notación diagramática para el caso de entidad empleadocon los atributos dni, nss, nombre, apellido y sueldo. |
Ejemplo de atributo univaluado
El atributo sueldo de la entidad empleado, por ejemplo, toma valores del dominio de los reales y únicamente toma un valor para cada empleado concreto; por lo tanto, ningún empleado puede tener más de un valor para el sueldo.
Como ya hemos comentado anteriormente, una entidad debe ser distinguible del resto de objetos del mundo real. Esto hace que para toda entidad sea posible encontrar un conjunto de atributos que permitan identificarla. Este conjunto de atributos forma una clave de la entidad.
Ejemplo de clave
La entidad empleado tiene una clave que consta del atributo dni porque todos los empleados tienen números de DNI diferentes.
Una determinada entidad puede tener más de una clave; es decir, puede tener varias claves candidatas.
| Los conceptos de clave candidata y clave primaria de una entidad son similares a los conceptos de clave candidata y clave primaria de una relación, que hemos estudiado en la unidad “El modelo relacional y el álgebra relacional”. |
Ejemplo de clave candidata
La entidad empleado tiene dos claves candidatas, la que está formada por el atributo dni y la que está constituida por el atributo nss, teniendo en cuenta que el NSS también será diferente para cada uno de los empleados.
El diseñador elige una clave primaria entre todas las claves candidatas. En la notación diagramática, la clave primaria se subraya para distinguirla del resto de las claves.
Ejemplo de clave primaria
En el caso de la entidad empleado, podemos elegir dni como clave primaria. En la figura del margen vemos que la clave primaria se subraya para distinguirla del resto.
Se define interrelación como una asociación entre entidades.Las interrelaciones se representan en los diagramas del modelo ER mediante un rombo. Junto al rombo se indica el nombre de la interrelación con letras mayúsculas.
Ejemplo de interrelación
Consideremos una entidad empleado y una entidad despacho y supongamos que a los empleados se les asignan despachos donde trabajar. Entonces hay una interrelación entre la entidad empleado y la entidad despacho.
Esta interrelación, que podríamos denominar asignación, asocia a los empleados con los despachos donde trabajan. La figura del margen muestra la interrelación asignación entre las entidades empleado y despacho.
El término interrelación se puede utilizar tanto para denominar asociaciones concretas u ocurrencias de asociaciones como para designar conjuntos o clases de asociaciones similares.
Ejemplo
Una interrelación se aplica tanto a una asociación concreta entre el empleado de DNI ‘50.455.234’ y el despacho ‘Diagonal, 20’ como a la asociación genérica entre la entidad empleado y la entidad despacho.
En ocasiones interesa reflejar algunas propiedades de las interrelaciones. Por este motivo, las interrelaciones pueden tener también atributos. Los atributos de las interrelaciones, igual que los de las entidades,tienen un cierto dominio, deben tomar valores atómicos y deben ser univaluados.Los atributos de las interrelaciones se representan mediante su nombre en minúsculas unido con un guión al rombo de la interrelación a la que pertenecen.
Ejemplo de atributo de una interrelación
Observemos la entidad estudiante y la entidad asignatura que se muestran en la figura siguiente:

Entre estas dos entidades se establece la interrelación evaluación para indicar de qué asignaturas han sido evaluados los estudiantes. Esta interrelación tiene el atributo nota, que sirve para especificar qué nota han obtenido los estudiantes de las asignaturas evaluadas.
Conviene observar que el atributo nota deber ser forzosamente un atributo de la interrelación evaluación, y que no sería correcto considerarlo un atributo de la entidad estudiante o un atributo de la entidad asignatura. Lo explicaremos analizando las ocurrencias de la interrelación evaluación que se muestran en la figura anterior.
Si nota se considerase un atributo de estudiante, entonces para el estudiante ‘E1’ de la figura necesitaríamos dos valores del atributo, uno para cada asignatura que tiene el estudiante; por lo tanto, no sería univaluado. De forma similar, si nota fuese atributo de asignatura tampoco podría ser univaluado porque, por ejemplo, la asignatura ‘A1’ requeriría tres valores de nota, una para cada estudiante que se ha matriculado en ella. Podemos concluir que el atributo nota está relacionado al mismo tiempo con una asignatura y con un estudiante que la cursa
y que, por ello, debe ser un atributo de la interrelación que asocia las dos entidades.
2.1.2. Grado de las interrelaciones
2.1.2. Grado de las interrelaciones Dataprix 28 Septiembre, 2009 - 10:58Una interrelación puede asociar dos o más entidades. El número de entidades que asocia una interrelación es el grado de la interrelación.Interrelaciones de grado dos
Las interrelaciones evaluación y asignación de los ejemplos anteriores tienen grado dos:
• La interrelación evaluación asocia la entidad estudiante y la entidad asignatura; es decir, asocia dos entidades.
• De forma análoga, la interrelación asignación asocia empleado y despacho.
Las interrelaciones de grado dos se denominan también interrelaciones binarias. Todas las interrelaciones de grado mayor que dos se denominan, en conjunto, interrelaciones n-arias. Así pues, una interrelación n-aria puede tener grado tres y ser una interrelación ternaria, puede tener grado cuatro y ser una interrelación cuaternaria, etc.
A continuación presentaremos un ejemplo que nos ilustrará el hecho de que, en ocasiones, las interrelaciones binarias no nos permiten modelizar correctamente la realidad y es necesario utilizar interrelaciones mayor grado.

Consideremos la interrelación evaluación de la figura anterior, que tiene un atributo nota. Este atributo permite registrar la nota obtenida por cada estudiante en cada asignatura de la que ha sido evaluado. Una interrelación permite establecer una sola asociación entre unas entidades individuales determinadas. En otras palabras, sólo se puede interrelacionar una vez al estudiante ‘E1’ con la asignatura ‘A1’ vía la interrelación evaluación.
Observad que, si pudiese haber más de una interrelación entre el estudiante ‘E1’ y la asignatura ‘A1’, no podríamos distinguir estas diferentes ocurrencias de la interrelación. Esta restricción hace que se registre una sola nota por estudiante y asignatura.
Supongamos que deseamos registrar varias notas por cada asignatura y estudiante correspondientes a varios semestres en los que un mismo estudiante ha cursado una asignatura determinada (desgraciadamente, algunos estudiantes tienen que cursar una asignatura varias veces antes de aprobarla). La interrelación anterior no nos permitiría reflejar este caso. Sería necesario aumentar el grado de la interrelación, tal y como se muestra en la figura siguiente:
La interrelación ternaria evaluación-semestral asocia estudiantes, asignaturas y una tercera entidad que denominamos semestre. Su atributo nota nos permite reflejar todas las notas de una asignatura que tiene un estudiante correspondientes a diferentes semestres.
De hecho, lo que sucede en este caso es que, según los requisitos de los usuarios de esta BD, una nota pertenece al mismo tiempo a un estudiante, a una asignatura y a un semestre y, lógicamente, debe ser un atributo de una interrelación ternaria entre estas tres entidades.
Este ejemplo demuestra que una interrelación binaria puede no ser suficiente para satisfacer los requisitos de los usuarios, y puede ser necesario aplicar una interrelación de mayor grado. Conviene observar que esto también puede ocurrir en interrelaciones que no tienen atributos.
Ejemplo de interrelación ternaria sin atributos
Consideremos un caso en el que deseamos saber para cada estudiante qué asignaturas ha cursado cada semestre, a pesar de que no queremos registrar la nota que ha obtenido. Entonces aplicaríamos también una interrelación ternaria entre las entidades estudiante, asignatura y semestre que no tendría atributos, tal y como se muestra en la figura siguiente:

Hemos analizado casos en los que era necesario utilizar interrelaciones ternarias para poder modelizar correctamente ciertas situaciones de interés del mundo real. Es preciso remarcar que, de forma similar, a veces puede ser necesario utilizar interrelaciones de grado todavía mayor: cuaternarias, etc.
En el subapartado siguiente analizaremos con detalle las interrelaciones binarias, y más adelante, las interrelaciones n-arias.
2.1.3. Interrelaciones binarias
2.1.3. Interrelaciones binarias Dataprix 28 Septiembre, 2009 - 11:28Conectividad de las interrelaciones binarias
La conectividad de una interrelación expresa el tipo de correspondencia que se establece entre las ocurrencias de entidades asociadas con la interrelación. En el caso de las interrelaciones binarias, expresa el número de ocurrencias de una de las entidades con las que una ocurrencia
de la otra entidad puede estar asociada según la interrelación.Una interrelación binaria entre dos entidades puede tener tres tipos de conectividad:
• Conectividad uno a uno (1:1). La conectividad 1:1 se denota poniendo un 1 a lado y lado de la interrelación.
• Conectividad uno a muchos (1:N). La conectividad 1:N se denota poniendo un 1 en un lado de la interrelación y una N en el otro.
• Conectividad muchos a muchos: (M:N). La conectividad M:N se denota poniendo una M en uno de los lados de la interrelación, y una N en el otro.
Ejemplos de conectividad en una interrelación binaria
A continuación analizaremos un ejemplo de cada una de las conectividades posibles para una interrelación binaria:
a) Conectividad 1:1

La interrelación anterior tiene conectividad 1:1. Esta interrelación asocia las delegaciones de una empresa con las ciudades donde están situadas. El hecho de que sea 1:1 indica que una ciudad tiene sólo una delegación, y que una delegación está situada en una única ciudad.
b) Conectividad 1:N

La interrelación asignación entre la entidad empleado y la entidad despacho tiene conectividad 1:N, y la N está en el lado de la entidad empleado. Esto significa que un empleado tiene un solo despacho asignado, pero que, en cambio, un despacho puede tener uno o más empleados asignados.
c) Conectividad M:N
Para analizar la conectividad M:N, consideramos la interrelación evaluación de la figura anterior. Nos indica que un estudiante puede ser evaluado de varias asignaturas y, al mismo tiempo, que una asignatura puede tener varios estudiantes por evaluar.
Es muy habitual que las interrelaciones binarias M:N y todas las n-arias tengan atributos. En cambio, las interrelaciones binarias 1:1 y 1:N no tienen por qué tenerlos. Siempre se pueden asignar estos atributos a la entidad del lado N, en el caso de las 1:N, y a cualquiera de las dos entidades interrelacionadas en el caso de las 1:1. Este cambio de situación del atributo se puede hacer porque no origina un atributo ultivaluado.
Dependencias de existencia en las interrelaciones binarias
En algunos casos, una entidad individual sólo puede existir si hay como mínimo otra entidad individual asociada con ella mediante una interrelación binaria determinada. En estos casos, se dice que esta última entidad es una entidad obligatoria en la interrelación. Cuando esto no sucede, se dice que es una entidad opcional en la interrelación.En el modelo ER, un círculo en la línea de conexión entre una entidad y una interrelación indica que la entidad es opcional en la interrelación. La obligatoriedad de una entidad a una interrelación se indica con una línea perpendicular. Si no se consigna ni un círculo ni una línea perpendicular, se considera que la dependencia de existencia es desconocida.
Ejemplo de dependencias de existencia
La figura siguiente nos servirá para entender el significado práctico de la dependencia de existencia. La entidad empleado es obligatoria en la interrelación dirección. Esto indica que no puede existir un departamento que no tenga un empleado que actúa de director del departamento. La entidad departamento, en cambio, es opcional en la interrelación dirección. Es posible que haya un empleado que no está interrelacionado con ningún departamento: puede haber –y es el caso más frecuente– empleados que no son directores de departamento.
Aplicaremos la dependencia de existencia en las interrelaciones binarias, pero no en las n-arias.
2.1.4. Ejemplo: base de datos de casas de colonias
2.1.4. Ejemplo: base de datos de casas de colonias Dataprix 28 Septiembre, 2009 - 12:04En este punto, y antes de continuar explicando construcciones más complejas del modelo ER, puede resultar muy ilustrativo ver la aplicación práctica de las construcciones que hemos estudiado hasta ahora. Por este motivo, analizaremos un caso práctico de diseño con el modelo ER que corresponde a una base de datos destinada a la gestión de las inscripciones en un conjunto de casas de colonias. El modelo ER de esta base de datos será bastante sencillo e incluirá sólo entidades, atributos e interrelaciones binarias (no incluirá interrelaciones n-arias ni otros tipos de estructuras).
La descripción siguiente explica con detalle los requisitos de los usuarios que hay que tener en cuenta al hacer el diseño conceptual de la futura base de datos:
a) Cada casa de colonias tiene un nombre que la identifica. Se desea saber de cada una, aparte del nombre, la capacidad (el número de niños que se pueden alojar en cada una como máximo), la comarca donde está situada y las ofertas de actividades que proporciona. Una casa puede ofrecer actividades como por ejemplo natación, esquí, remo, pintura, fotografía, música, etc.
b) Es necesario tener en cuenta que en una casa de colonias se pueden practicar varias actividades (de hecho, cada casa debe ofrecer como mínimo una), y también puede ocurrir que una misma actividad se pueda llevar a cabo en varias casas. Sin embargo, toda actividad que se registre en la base de datos debe ser ofertada como mínimo en una de las casas.
| Es posible, ... |
| ... por ejemplo, que una actividad como por ejemplo el esquí tenga una calificación de 10 en la oferta de la casa Grévol, y que la misma actividad tenga una calificación de 8 en la casa Ardilla. |
c) Interesa tener una evaluación de las ofertas de actividades que proporcionan las casas. Se asigna una calificación numérica que indica el nivel de calidad que tiene cada una de las actividades ofertadas.
d) Las casas de colonias alojan niños que se han inscrito para pasar en ellas unas pequeñas vacaciones. Se quiere tener constancia de los niños que se alojan en cada una de las casas en el momento actual. Se debe suponer que hay casas que están vacías (en las que no se aloja ningún niño) durante algunas temporadas.
e) De los niños que se alojan actualmente en alguna de las casas, interesa conocer un código que se les asigna para identificarlos, su nombre, su apellido, el número de teléfono de sus padres y su comarca de residencia.
f) De las comarcas donde hay casas o bien donde residen niños, se quiere tener registrados la superficie y el número de habitantes. Se debe considerar que puede haber comarcas donde no reside ninguno de los niños que se alojan en un momento determinado en las casas de colonias, y comarcas que no disponen de ninguna casa.
La figura siguiente muestra un diagrama ER que satisface los requisitos anteriores. Los atributos de las entidades no figuran en el diagrama y se listan aparte.
Los atributos de las entidades que figuran en el diagrama son los siguientes (las claves primarias están subrayadas):
A continuación comentamos los aspectos más relevantes de este modelo ER:
1) Una de las dificultades que en ocasiones se presenta durante la modeliza ción conceptual es decidir si una información determinada debe ser una entidad o un atributo. En nuestro ejemplo, puede resultar difícil decidir si comarca se debe modelizar como una entidad o como un atributo.
A primera vista, podría parecer que comarca debe ser un atributo de la entidad casa-colonias para indicar dónde está situada una casa de colonias, y también un atributo de la entidad niño para indicar la residencia del niño. Sin embargo, esta solución no sería adecuada, porque se quieren tener informaciones adicionales asociadas a la comarca: la superficie y el número de habitantes. Es preciso que comarca sea una entidad para poder reflejar estas informaciones adicionales como atributos de la entidad.
La entidad comarca tendrá que estar, evidentemente, interrelacionada con las entidades niño y casa-colonias. Observad que de este modo, además, se hace patente que las comarcas de residencia de los niños y las comarcas de situación de las casas son informaciones de un mismo tipo.
2) Otra decisión que hay que tomar es si el concepto actividad se debe modelizar como una entidad o como un atributo. Actividad no tiene informaciones adicionales asociadas; no tiene, por lo tanto, más atributos que los que forman la clave. Aun así, es necesario que actividad sea una entidad para que, mediante la interrelación oferta, se pueda indicar que una casa de colonias ofrece actividades.
Observad que las actividades ofertadas no se pueden expresar como un atributo de casa-colonias, porque una casa puede ofrecer muchas actividades y, en este caso, el atributo no podría tomar un valor único.
3) Otra elección difícil, que con frecuencia se presenta al diseñar un modelo ER, consiste en modelizar una información determinada como una entidad o como una interrelación. Por ejemplo, podríamos haber establecido que oferta, en lugar de ser una interrelación, fuese una entidad; lo habríamos hecho así:
La entidad oferta representada en la figura anterior tiene los atributos que presentamos a continuación:
Esta solución no acaba de reflejar adecuadamente la realidad. Si analizamos la clave de oferta, podemos ver que se identifica con nombre-casa, que es la clave de la entidad casa-colonias, y con nombre-actividad, que es la clave de la entidad actividad. Esto nos debe hacer sospechar que oferta, de hecho, corresponde a una asociación o interrelación entre casas y actividades. En consecuencia, reflejaremos la realidad con más exactitud si modelizamos oferta como una interrelación entre estas entidades.
4) Finalmente, un aspecto que hay que cuidar durante el diseño conceptual es el de evitar las redundancias. Por ejemplo, si hubiésemos interrelacionado comarca con actividad para saber qué actividades se realizan en las casas de cada una de las comarcas, habríamos tenido información redundante. La interrelación oferta junto con la interrelación situación ya permiten saber, de forma indirecta, qué actividades se hacen en las comarcas.
2.1.5. Interrelaciones n-arias
2.1.5. Interrelaciones n-arias Dataprix 29 Septiembre, 2009 - 09:55Las interrelaciones n-arias, igual que las binarias, pueden tener diferentes tipos de conectividad. En este subapartado analizaremos primero el caso particular de las interrelaciones ternarias y, a continuación, trataremos las conectividades de las interrelaciones n-arias en general.
Conectividad de las interrelaciones ternarias
| Observad que usamos M, N y P para representar “muchos”, y 1 para representar “uno”. |
Cada una de las tres entidades asociadas con una interrelación ternaria
puede estar conectada con conectividad “uno” o bien con conectividad
“muchos”. En consecuencia, las interrelaciones ternarias pueden tener
cuatro tipos de conectividad: M:N:P, M:M:1, N:1:1 y 1:1:1.
Analizaremos cómo se decide cuál es la conectividad adecuada de una interrelación ternaria mediante el siguiente ejemplo. Consideremos una interrelación que denominamos clase y que asocia las entidades asignatura, aula y hora-semanal. Esta interrelación permite registrar clases presenciales. Una clase corresponde a una asignatura determinada, se imparte en un aula determinada y a una hora de la semana determinada. Por ejemplo, podemos registrar que se hace clase de la asignatura IBD en el aula D222 el martes a las 9, tal y como se muestra en la figura de la página siguiente. El atributo duración nos permite saber cuántas horas dura la clase.
Para decidir si el lado de la entidad asignatura se conecta con “uno” o con “muchos” , es necesario preguntarse si, dadas un aula y una hora-semanal, se puede hacer clase de sólo una o bien de muchas asignaturas en aquellas aula y hora. La respuesta sería que sólo se puede hacer clase de una asignatura en una misma aula y hora. Esto nos indica que asignatura se conecta con “uno”, tal y como reflejamos en la figura siguiente:
Como nos indica este ejemplo, para decidir cómo se debe conectar una de las entidades, es necesario preguntarse si, ya fijadas ocurrencias concretas de las otras dos, es posible conectar sólo “una” o bien “muchas” ocurrencias de la primera entidad.
Utilizaremos el mismo procedimiento para determinar cómo se conectan las otras dos entidades del ejemplo. Una vez fijadas una asignatura y un aula, es posible que se haga clase de aquella asignatura en aquella aula, en varias horas de la semana; entonces, hora-semana se conecta con “muchos”. Finalmente, la entidad aula se conecta con “uno”, teniendo en cuenta que, fijadas una asignatura y una hora de la semana, sólo se puede hacer una clase de aquella asignatura a aquella hora. La conectividad resultante, de este modo, es N:1:1.
Caso general: conectividad de las interrelaciones n-arias
Lo que hemos explicado sobre la conectividad para las interrelaciones ternarias es fácilmente generalizable a interrelaciones n-arias.
| * Recordad que para las interrelaciones ternarias hay cuatro tipos posibles de conectividad. |
Una interrelación n-aria puede tener n + 1 tipos de conectividad, teniendo en cuenta que cada una de las n entidades puede estar conectada con “uno” o con “muchos” en la interrelación*. Para decidir si una de las entidades se conecta con “uno” o con “muchos”, es necesario preguntarse si, fijadas ocurrencias concretas de las otras n – 1 entidades, es posible conectar sólo una o bien muchas ocurrencias de la primera entidad:
• Si la respuesta es que sólo una, entonces se conecta con “uno”.
• Si la respuesta es que muchas, la entidad se conecta con “muchos”.
2.1.6. Interrelaciones recursivas
2.1.6. Interrelaciones recursivas Dataprix 29 Septiembre, 2009 - 10:13Una interrelación recursiva es una interrelación en la que alguna entidad está asociada más de una vez.Ejemplo de interrelación recursiva
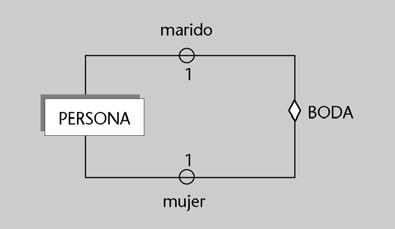
Si, para una entidad persona, queremos tener constancia de qué personas están actualmente casadas entre ellas, será necesario definir la siguiente interrelación, que asocia dos veces la entidad persona:

Una interrelación recursiva puede ser tanto binaria como n-aria:
| * Éste es el caso de la interrelación boda anterior. |
1) Interrelación recursiva binaria: interrelación en la que las ocurrencias asocian dos instancias de la misma entidad*. Las interrelaciones binarias recursivas pueden tener conectividad 1:1, 1:N o M:N, como todas las binarias. En esta interrelación también es posible expresar la dependencia de existencia igual que en el resto de las interrelaciones binarias
Ejemplo de interrelación recursiva binaria
La interrelación boda tiene conectividad 1:1 porque un marido está casado con una sola mujer y una mujer está casada con un solo marido. También tiene un círculo en los dos lados
(según la dependencia de existencia), porque puede haber personas que no estén casadas.
En una interrelación recursiva, puede interesar distinguir los diferentes papeles que una misma entidad tiene en la interrelación. Con este objetivo, se puede etiquetar cada línea de la interrelación con un rol. En las interrelaciones no recursivas normalmente no se especifica el rol; puesto que todas las entidades interrelacionadas son de clases diferentes, sus diferencias de rol se sobreentienden.
Roles diferentes
Una ocurrencia de la interrelación boda asocia a dos personas concretas. Para reflejar el papel diferente que tiene cada una de ellas en la interrelación, una de las personas tendrá el rol de marido y la otra tendrá el rol de mujer.
Algunas interrelaciones recursivas no presentan diferenciación de roles; entonces, las líneas de la interrelación no se etiquetan.
No-diferencia de roles
Consideremos una interrelación amistad que asocia a personas concretas que son amigas. A diferencia de lo que sucedía en la interrelación boda, donde una de las personas es el marido y la otra la mujer, en este caso no hay diferenciación de roles entre las dos personas interrelacionadas. A continuación se muestra esta interrelación. Observad que su conectividad es M:N, teniendo en cuenta que una persona puede tener muchos amigos y, al mismo tiempo, puede haber muchas personas que la consideran amiga.

2) Interrelación recursiva n-aria: interrelación recursiva en la que las ocurrencias asocian más de dos instancias.
Ejemplo de interrelación recursiva ternaria
Consideremos una interrelación que registra todas las bodas que se han producido a lo largo del tiempo entre un conjunto de personas determinado. Esta interrelación permite tener constancia no sólo de las bodas vigentes, sino de todas las bodas realizadas en un cierto periodo de tiempo.
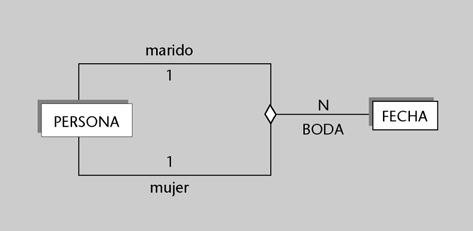
Esta interrelación es recursiva y ternaria. Una ocurrencia de la interrelación asocia a una persona que es el marido, a otra que es la mujer y la fecha de su boda. La conectividad es N:1:1.
A los lados del marido y de la mujer les corresponde un 1, porque un marido o una mujer, en una fecha determinada, se casa con una sola persona. Al lado de la entidad fecha le corresponde una N, porque se podría dar el caso de que hubiese, en fechas diferentes, más de una boda entre las mismas personas.
2.1.7. Entidades debiles
2.1.7. Entidades debiles Dataprix 29 Septiembre, 2009 - 10:21Las entidades que hemos considerado hasta ahora tienen un conjunto de atributos que forman su claves primarias y que permiten identificarlas completamente. Estas entidades se denominan, de forma más específica, entidades fuertes. En este subapartado consideraremos otro tipo de entidades que denominaremos entidades débiles.
Una entidad débil es una entidad cuyos atributos no la identifican completamente, sino que sólo la identifican de forma parcial. Esta entidad debe participar en una interrelación que ayuda a identificarla.Una entidad débil se representa con un rectángulo doble, y la interrelación que ayuda a identificarla se representa con una doble línea.
Ejemplo de entidad débil
Consideremos las entidades edificio y despacho de la figura siguiente. Supongamos que puede haber despachos con el mismo número en edificios diferentes. Entonces, su número no identifica completamente un despacho. Para identificar completamente un despacho, es necesario tener en cuenta en qué edificio está situado. De hecho, podemos identificar un despacho mediante la interrelación situación, que lo asocia a un único edificio. El nombre del edificio donde está situado junto con el número de despacho lo identifican completamente.

En el ejemplo anterior, la interrelación situación nos ha permitido completar la identificación de los despachos. Para toda entidad débil, siempre debe haber una única interrelación que permita completar su identificación. Esta interrelación debe ser binaria con conectividad 1:N, y la entidad débil debe estar en el lado N. De este modo, una ocurrencia de la entidad débil está asociada con una sola ocurrencia de la entidad del lado 1, y será posible completar su identificación de forma única. Además, la entidad del lado 1 debe ser obligatoria en la interrelación porque, si no fuese así, alguna ocurrencia de la entidad débil podría no estar interrelacionada con ninguna de sus ocurrencias y no se podría identificar completamente.